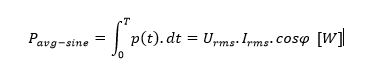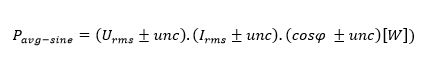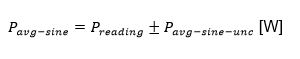The effect of internal phase shift on power measurement

The contribution of the measuring instrument’s internal phase-shift uncertainty to the total power measurement uncertainty is often over-looked. The amount of electrical energy that is transmitted, stored or converted relates directly to the voltage and current involved. This can be expressed by the formula:

 p(t) = u(t).i(t) [VA]

with the time relationship indicating that the general formula is valid only for instantaneous measurements.

If the application is an ideal, continuous and stable sine-wave energy conversion, the following formula is used to calculate the average power:

The main reason for integration in the above equation is to calculate the average power over the total period T.

The uncertainty of each of the factors contributes to the total uncertainty:

Following the standard method for total uncertainty calculation, the relative uncertainty of the power reading can be written as:

Where ∆U, ∆I & ∆cos φ represent the uncertainty of the voltage, current and power factor respectively.

As can be seen from this equation, the power-factor (cosφ) uncertainty is a significant factor for the correct measurement of power: as important as the RMS values of the voltage and current.

Finally, the power measurement can be expressed as:

This article will concentrate on the contribution, the internal cosφ uncertainty of the measurement instrument itself and its contribution to the total power measurement uncertainty.

Internal phase shift uncertainty

If the applied voltage and current are beyond the direct input capabilities of the power meter, external voltage and current sensors are used to attenuate or amplify the signals to bring them within the guaranteed input measurement ranges of the instrument. Every link in the chain contributes to an increase in the total uncertainty value, including an external phase shift in both the voltage and current sensor, which has to be added to the power meter internal uncertainty.

A typical electric power measurement involves a two-channel instrument with a perfect phase synchronisation between the two channels. One channel measures the voltage across the load, while the other channel measures the current through the load. The signals paths of both channels are through the electric circuitry in the front end of the power meter, and will have unequal delays. The voltage (e.g. 1,000V) is attenuated to a level that the ADC can handle (e.g. 3V), while the small voltage drop across the current shunt (µV) needs amplification (to e.g. 3V) for the same reason. The challenge for the power-meter design engineer is to achieve this normalisation process for signals from DC up to 1MHz without any additional phase delays.

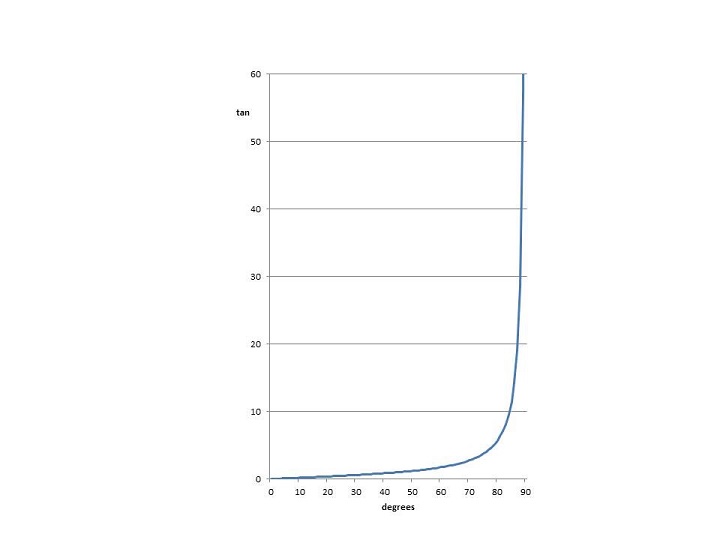
Figure 1: The limitation of the internal net phase delay is a major goal for the power meter design engineer

It is the net delay (the difference between the delay of the voltage and the current inputs) from the input connectors to the ADC that causes the internal phase uncertainty.

The symbol for this quantity is δ, and it is expressed in radians for a specific frequency.

Most multi-channel instruments do not have any channel-delay value in product specifications. This means that these instruments are not suitable for making high-precision electric power measurements.

The internal phase uncertainty should always be included in high-precision power measurements. Depending on the external phase shift φ, caused by the load, the contribution of the internal phase shift uncertainty δ can vary from negligible (where PF = cosφ = 1) to very dominant (where PF = cosφ < 0.01).

The instrument’s internal phase uncertainty means this factor needs to be added to the total power reading:

Total power uncertainty

This formula demonstrates an increasing effect of δ on the total power uncertainty as the external phase shift increases from 0̊ to 90̊ (Figure 1). Consequently, power measuring instruments with smaller internal phase-shift uncertainties are more expensive. The limitation of the internal net phase delay is a major goal for the power meter design engineer.

The role of the internal instrument uncertainty increases when the phase difference between the voltage across the load and current through the load is approaching 90̊. This situation is typically found in stand-by power measurements and transformer loss measurement applications.

Figure 2: The Precision Power Scope is part of Yokogawa’s power meters and analysers range

The signal delays of both voltage and current signals are also frequency dependant, each frequency will have a specific value of δ. This means that, for distorted voltage and current signals, each frequency power component has to be measured before its contribution to the total power uncertainty can be assessed. A PLL (phase locked loop) based on the FFT can generate these values, including uncertainty values for each frequency power component.

The internal phase-shift uncertainty is clearly an important specification in precision power measurement, and yet the specifications of many power measuring instruments do not mention it at all.  Yokogawa is the only manufacturer of power meters and analysers (including the Precision Power Scope, Figure 2) to specify the internal phase shift uncertainty.